Marco Bussagli, storico dell’ arte, docente, pittore e giornalista, attraverso il prestito di opere offerto dalla Collezione Giudiceandrea e col supporto della Fondazione Escher ha concepito e curato la monografica di Maurits Cornelis Escher (Leeuwarden, 17 giugno 1898 – Laren, 27 marzo 1972) al Chiostro del Bramante di Roma, co-prodotta in collaborazione con Arthemisia Group (catalogo Skira). Lo abbiamo incontrato e a lui abbiamo chiesto di approfondire l’artista, la ricerca alla base del suo complesso lavoro e la mostra.
Il fenomeno Escher condiziona(va) da tempo la sua corretta percezione. Moltissimo è spiegato nel catalogo monografico. In questo senso l’esposizione da te curata segna un punto di rottura e partenza.
“Escher, spesso e volentieri, è stato considerato una sorta di capriccio della storia dell’arte, un incisore che non è detto che sia un artista e, soprattutto, un uomo cervellotico che, a dispetto delle sue fissazioni matematiche, ha avuto un notevole successo di pubblico. Non più tardi di sei anni or sono, nel 2008, si tenne a Vienna presso il Mumok la mostra intitolata Genau und anders, ossia precisione e altro, dedicata al rapporto fra matematica ed arte, da Albrecht Dürer a Sol Le Witt, che vide la clamorosa esclusione di Escher, con l’incredibile giustificazione, scritta nero su bianco sul catalogo, che la sua produzione non poteva considerarsi arte. Bene, la mostra Escher al Chiostro del Bramante è la risposta a quell’esclusione. Come giustamente è implicito nella domanda, il fenomeno Escher, ossia la diffusione planetaria delle sue immagini, riprodotte su poster, magliette, tazze da thè, matite e gadget di ogni tipo, per non parlare dei siti web, ha impedito che si fosse attenti alla sua dimensione artistica che non ha nulla da invidiare a quella dei grandi contemporanei del XX secolo, da Dalì a Picasso, tanto per fare due nomi altisonanti. Non per nulla, in mostra, ci sono molti riferimenti ad artisti a lui vicini, oppure con i quali non è difficile trovare una evidente relazione, da De Chirico a Duchamp, passando per le opere di Luca Patelle che ha battuto terreni comuni tanto all’incisore olandese, quanto all’artista francese.”
Escher abitava in una casa del XVII secolo. Qual è la chiave di lettura per capire il rapporto tra l’ambiente e la famiglia di origine dell’artista e il particolare orientamento del suo modernissimo talento? Nel catalogo ricordi il trompe-l’oeil nordico, le geometrie arabe. Ma anche le consonanze con il lavoro di Hieronymus Bosch. Escher aveva una notevole cultura visiva ed artistica: da Pozzo a Dalì, sono molti i riferimenti che indichi nel tuo saggio.
“Come giustamente hai evidenziato, Escher aveva un’enorme cultura visiva, nata per sedimentazioni che sono di certo state favorite dall’ambiente in cui è vissuto, ovvero quello di una famiglia benestante, capace di assecondare le sue inclinazioni e i suoi interessi senza dover affrontare affanni economici. Il padre, ingegnere edile, avrebbe voluto che il piccolo Maurits, detto Mauck, avesse continuato la professione paterna, ma il futuro artista non aveva una particolare inclinazione per lo studio scolastico. Prese la licenza liceale con una certa difficoltà e anche la carriera universitaria fu poco brillante e subito interrotta. Escher trovò la sua strada grazie alla cura e all’insegnamento di Samuel Jessurum de Mesquita, un abile incisore che gli insegnò tutte le tecniche e lo iniziò ai segreti della xilografia, il mezzo più frequentato dal grande olandese. Di origine ebraica (morì nel campo di concentramento di Auschwitz), de Mesquita aveva assorbito la felice leggerezza ornamentale dell’Art Nouveau, i cui gusto condizionò non poco i primi passi del giovane Escher. L’idea della tassellazione, infatti, viene da qui, da quel gusto per le carte da parati decorate a motivi geometrici e floreali che si ripetono come all’infinito e che si basano su uno schema geometrico semplice, ma efficace. In mostra c’è un capolavoro del Novecento, la cartella di litografie progettate da Koloman Moser, uno degli esponenti principali della Secessione viennese, che costituiscono un prontuario per utilizzare carte da parati, stoffe per mobili, carte da risguardi, di cui Moser ha raccolto ben sessanta motivi decorativi. E’ intitolata Die Quelle (questo il nome della cartella) che, appunto, vuol dire la fonte, dei motivi decorativi, naturalmente, come recita il sottotitolo tedesco: flächenschmuck. Bene, ce ne sono alcuni che sembrano delle opere dell’Escher maturo ante litteram. L’artista olandese non ha mai conosciuto Die Quelle nel corso della sua formazione, ma la cartella di Moser esemplifica certamente quello che era il gusto art-nouveau di quegli anni, quando il giovane Escher andava a lezione da de Mesquita. La formazione di Escher, però, non va confinata a quel periodo, ma continuò e si perfezionò nel corso del suo lungo soggiorno italiano…”
…il diario del viaggio in Italia. Escher disegnava viaggiando. Poi nel 1935 lasciò l’Italia (fu a Roma, tra 1927 e 1935).
“Sì, Escher giunse per la prima volta in Italia nel 1922, insieme ai genitori che gli organizzarono un viaggio per contrastare la sua depressione. Il futuro artista s’innamorò del nostro paese che definì «luogo benedetto». Qui ebbe la fortuna di conoscere sua moglie Giulietta Umiker, milanese nonostante il cognome, detta “Jetta”, che sarà l’amore di tutta una vita e uno dei suoi più cari amici, Joseph Haas de Triverio, con il quale condivise i viaggi a dorso di mulo, in treno e a piedi in tutta Italia, dall’Abruzzo amatissimo alla Calabria, fino a Palermo. Partivano in primavera, disegnavano e, in tarda estate, cominciavano ad incidere. Di Triverio in mostra c’è un autoritratto e una sua incisione. L’Italia, però, offrì ad Escher ampie possibilità professionali. La prima mostra personale fu a Siena nell’agosto del 1923. Poi Triverio lo guidò nell’ambiente romano introducendolo nei circuiti espositivi. L’altra figura importante per l’ artista a Roma fu Goedefridus Johannes Hoogewerff, il direttore dell’Istituto di Cultura Olandese a Roma. Escher apparteneva all’alta borghesia olandese, abitava in via Poerio, zona Monteverde, ed era quindi in contatto con i più qualificati connazionali presenti nella capitale. Entrò così in contatto con altri due personaggi fondamentali: Federico Hermanin e Adolfo Venturi. Il primo, una sorta di ministro dei Beni Culturali (il cui dicastero allora non esisteva, ma i cui interessi erano salvaguardati da quello dell’Istruzione) che gli organizzò, nel 1926, una mostra presso il prestigioso Gruppo Romano Artisti Incisori che aveva sede in Palazzo Venezia, ovvero nella sede stessa del Governo fascista. Del secondo, seguiva le lezioni all’Università ed approfondiva la conoscenza della Storia dell’Arte. Hoogewerff, infine, gli offrì occasioni di lavoro. Realizzarono insieme la serie degli Emblemata e gli fece fare un’ esposizione presso l’Istituto nel 1932. L’avventura italiana finì perché un bel giorno del 1935, quando Escher vide rientrare il figlio George vestito da Piccolo Balilla. Pensò che l’Italia stesse imboccando una strada sbagliata e, nel giro di sei mesi, lasciò il nostro paese, anche se -prima di partire- tenne un’altra personale presso l’Istituto Olandese di Cultura (1936) .
Il paesaggio è stato al centro del suo lavoro, nelle varianti della sua architettura visionaria e paradossale e della micro-architettura della natura (foglie, ramarro, cristallo).
“Il paesaggio italiano è sempre stato nel cuore di Escher, dal giorno in cui mise piede al di qua delle Alpi. Quando dovette lasciare la nostra penisola, lo fece a malincuore e dichiarò più volte che, per colmare questo dolore, pensò di rivolgersi alle sue immagini interiori. L’approccio dell’artista olandese al paesaggio, però, non era né lirico né romantico, ma attento ad evidenziare quel reticolo geometrico che, per Escher, costituiva la struttura continua su cui si basano le molteplici ed apparentemente capricciose forme di una natura sorprendente. C’è un episodio che spiega bene questa impostazione assai personale e particolare. Nei suoi diari senesi, l’artista ha narrato di essere molto soddisfatto perché, fuori porta Camollia aveva trovato una postazione dalla quale riusciva a ridisegnare il Duomo della città da un punto di vista ortogonale. Il fatto ancor più sbalorditivo, è che dietro queste scelte dettate dalla sua visione geometrica del mondo, si scorge la passione che Escher aveva per il mistero dell’esistenza, per la magia della realtà che riesce anche oggi a squadernare con mezzi tanto semplici quanto efficaci. Un’opera come Metamorfosi II – una della più lunghe incisioni mai realizzate (quasi quattro metri di lunghezza), capolavoro della sua produzione – parte dall’idea che una forma possa scomparire nell’altra e trasformarsi passando dalle lucertole alle api, ai colibrì, dai pesci al paesaggio urbano (con il bellissimo duomo di Atrani, omaggio all’Italia ed alle tappe del proprio viaggio di nozze), fino alla scacchiera e di nuovo alla scritta. Metodo per questo percorso proteiforme è quello della tassellatura o piastrellazione che altro non è se non la regolare divisione del piano con uno stesso modulo che non è più una semplice forma geometrica, ma di volta in volta può essere un pesce, un uccello, un ramarro, un cavallo o un cavaliere, un cane o una formica. In questo modo, Escher dà forma a quello che Bergson chiamava élan vital e che certo l’artista rintracciava anche nella visione del mondo di Teilhard de Chardin che egli cita esplicitamente.”
Parlaci della Gestalt e delle sue leggi. Escher – la mostra lo chiarisce – crea le sue immagini partendo deliberatamente da esse.
“Per questo motivo, definire Escher semplicemente un artista è riduttivo. A lui si attaglia bene il termine intellettuale che non lo relega nel canto della creatività, ma ne considera anche l’aspetto speculativo, prepotente nell’opera del grande olandese. Del resto basta osservare i pacchi di quaderni e di fogli, gli studi sterminati che l’incisore ha affrontato per trovare questa o quella soluzione che non è solo la trovata più o meno geniale, ma l’applicazione di leggi geometriche, matematiche ed anche cristallografiche che sono alla base di quelle che, diversamente, potrebbero sembrare solo scelte formali. In questa ricerca, sicuramente, Escher è incappato nelle leggi della Gestalt, o della percezione visiva.
La locuzione tedesca Gestalttheorie, che vuole dire letteralmente «teoria della forma», indica una corrente di studio della psicologia finalizzata all’analisi delle modalità con le quali il cervello umano e l’occhio, inteso come strumento della percezione, riescono ad organizzare una visione coerente del mondo. Da questo processo di studio, iniziato verso il 1890 nelle Università di Vienna, Graz e Monaco di Baviera, poi proseguito in Germania, a Berlino e a Francoforte, fra il 1910 ed il 1930, sono scaturite una serie di regole che costituiscono, per l’appunto, la Gestalttheorie, successivamente sviluppata negli atenei degli Stati Uniti d’America, dove si trasferirono gli scienziati contrari al regime nazista. Escher, inoltre, si è sempre interessato del tema della cristallografia trovando come interlocutori privilegiati, forse anche il padre ingegnere; di sicuro il fratellastro Berend Geroge, cristallografo, con cui discusse le prime osservazioni sulla divisione regolare del piano. Più tardi, la Schattschneider che dedicò all’opera di Escher veri trattati di cristallografia. Del resto, i matematici ed i cristallografi amarono molto questo artista, a cominciare dal suo fraterno amico Bruno Ernst, che pubblicò molti libri sull’artista.
Le leggi prese in considerazioni sono le seguenti:
Legge della semplificazione.

La successione di queste tabelle dimostra che la collocazione di quattro punti su un piano a distanza regolare viene organizzata dal nostro cervello secondo lo schema più semplice che, in questo caso è quello del quadrato. Se poi si aggiungono altri quattro punto negli spazi fra un punto e l’altro, il risultato sarà quello di considerare l’insieme un cerchio. Un esempio sta nelle parti iniziali e finali di Metamorfosi II dove le lettere si organizzano in quadrati.

Legge della prossimità.
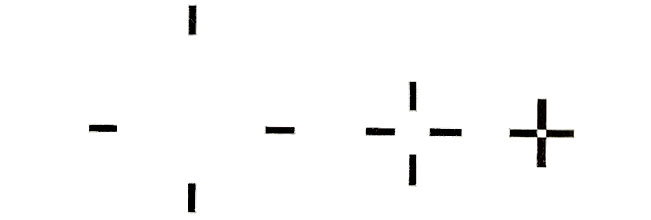
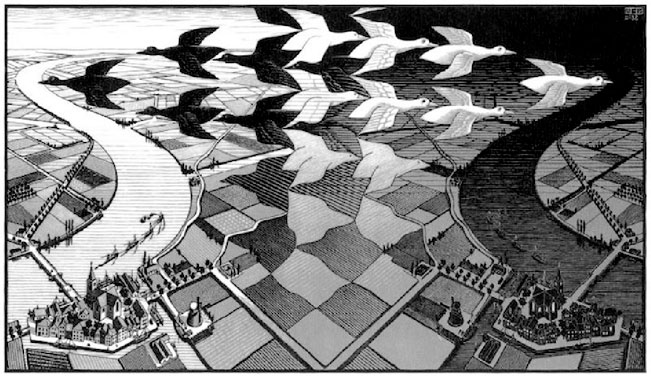
La tabella mostra come le quattro barrette, quando si avvicinano perdono la loro autonomia e il nostro cervello finisce per percepire la combinazione delle quattro barre, ossia una croce della quale non si percepiscono più le componenti originarie. Anche Escher sfrutta questa legge, anche se in maniera più complessa perché si combina con quella del “pieno e del vuoto” che esamineremo più avanti. Basterà, infatti, osservare Giorno e notte. Quando le anatre si avvicinano, il vuoto che compongono viene percepito come forma compiuta del pattern, ossia dell’anatra.
Legge della buona forma.

La percezione di più elementi su un piano che ne determino una divisione regolare, sono ricondotti alla forma più semplice, ossia la “buona forma”. Così, nel primo disegno, il modulo a “doppia coda di rondine” ripetuto sul piano finisce per generare la percezione di quadrati più grandi e quadrati più piccoli. Il medesimo fenomeno percettivo lo troviamo anche nel secondo disegno, dove la stella o croce di Malta scompare lasciando emergere un ‘tappeto’ di quadrati più grandi e più piccoli.

Pure Escher sfrutta questa legge, come mostra questa incisione giovanile, dove la simultanea di spicchi bianchi e neri non riesce a nascondere la presenza di un cerchio e di un quadrato inscritto che sono il vero soggetto della xilografia.
Legge della continuità.

Osservando la successione di biciclette sulla sinistra, a nessuno verrebbe in mente che fra queste ci sia un tandem. Al contrario, il sospetto, per non dire la certezza, viene nel disegno a destra. Il muro che copre la metà di ciascuna delle due bicilette centrali. Il nostro cervello, infatti, tende a considerare continuo quello che, in realtà, è separato, ma coperto. Quindi, noi tendiamo a legare un immagine all’altra per una percezione di continuità dello spazio.

Anche Escher utilizza questa legge per ammaliare con la sua magia. Non per nulla, questa litografia s’intitola Specchio magico e pare che il draghetto entri ed esca dallo specchio, quando invece, sono due i draghetti che creano quest’impressione: il riflesso delle terga di quello che curva a destra e il corpo di quello che, dietro lo specchio, gira a sinistra. Il nostro cervello, però, per la legge della continuità, considera il drago uno solo.
Legge del triangolo di Kanizsa.

Non è difficile percepire al centro di questo disegno un triangolo bianco che pare sovrastare quello dai bordi neri e i tre dischi rossi. In realtà, però, non esiste e non è mai stato disegnato. Al contrario, è il risultato dell’interazione visiva di dischi rossi cui manca uno spicchio e di angoli neri opportunamente collocati. Ad inventare e studiare l’immagine, fu Gaetano Kanisza, italiano di Trieste, a dispetto del nome, psicologo e pittore italiano che si dedicò a queste ricerche.

Anche Escher utilizza questa legge di percezione visiva che si basa sui contrasti simultanei. Qui, nel caso di Morano, la plastica e il volume delle case è restituito solo con il rapporto del bianco e nero.
Legge del pieno e del vuoto: il vaso di Rubin.

Quello del vaso di Rubin è un caso particolare del rapporto fra pieno e vuoto, dal momento che il vuoto al centro diviene un vaso concreto, ma il vuoto ai lati si configura come la chiara presenza di due profili umani che sono a loro volta il pieno se si considera vuoto il vaso, come accade nei Vasi fisiognomici di Luca Patella.
Il ricorso a questa legge della percezione visiva, in Escher è continua, quando si dedica al tema della divisione regolare del piano, dove il vuoto diviene il pieno di una lettura inversa del piano stesso.
Legge della percezione del convesso e del concavo.

È noto che delle scodelle illuminate dall’alto sembreranno tali, illuminate dal basso, invece, parranno sfere e illuminate di lato possono sembrare alternativamente l’una o l’altra cosa. Escher conosce bene questa legge e la utilizza magistralmente in un piccolo capolavoro che, non per caso s’intitola Concavo e convesso.

Le difficoltà di una seria e non superficiale comprensione di Escher sono superate nel catalogo, che offre una chiara opportunità di notevole valore pedagogico e scientifico per tanti, iniziati e non. Ad esempio, a proposito della geometria euclidea e non euclidea e delle soluzioni adottate da Escher nelle sue xilografie; o del numero irrazionale 1,6180 che è alla base della sezione aurea, dal Partenone alla Gioconda, fino all’Unité d’Abitation di Le Corbusier di Marsiglia.
“Ti ringrazio per l’apprezzamento del catalogo edito con grande cura da Skira e che contiene contributi prestigiosi, da quello di Federico Giudicenadrea, non solo appassionato di Escher, ma proprietario della più grande collezione di stampe del grande artista (il termine può comunque essere utilizzato) olandese, a l’altro di Luigi Grasselli, matematico di fama internazionale e pro-rettore dell’Università di Modena-Reggio Emilia. Lo scopo, infatti, è quello di offrire al grande pubblico gli strumenti per non fermarsi alla sola ammirazione per le incisioni di Maurits Cornelis Escher.”
Puoi spiegare ai nostri lettori l’ importanza di matematica e canone inverso nella musica, ma soprattutto per Escher e l’ ambito di cui ti sei occupato?
“Bisogna sapere che Douglas Hofstadter, professore di Scienza cognitiva e informatica presso l’Indiana University, ha scritto un testo ormai celebre Gödel, Escher, Bach: un’Eterna Ghirlanda Brillante, vincitore nel 1980 del Premio Pulitzer per la saggistica. Hofstadter mise insieme – con geniale intuizion e- un artista, un musicista e un matematico per spiegare quale sia la logica delle strutture sub-molecolari come il DNA, attraverso quello che lo studioso chiama Canone cancrizzante, ossia quella fusione di due concetti diversi che danno origine a qualche cosa di nuovo. Si tratta, come spiega, di «ricombinazione simbolica» come nel caso della parola «pomodoro», dove le due componenti «pomo» ed «oro» si fondono in un nuovo concetto che li contiene entrambi, ma che li supera completamente. Proprio come per il tedesco Handschuhe che vuol dire «guanti», ma che è composto dai termini hand ovvero «mano» e schuhe «scarpe». Tuttavia, la frase, il sistema, l’enunciato o la stringa da cui si parte, può subire una variazione che determina la sua ricomposizione speculare, come una sorta di palindromo. La variante è il Canone cancrizzante ed Hofstadter spiega con dovizia di particolari quale sia stato il suo percorso mentale per mettere a punto la soluzione che, come suo solito, ripropone in forma di dialogo fra Achille e la Tartaruga, i due protagonisti delle aporie del movimento enunciate dal filosofo greco Zenone, poi riprese da Lewis Carroll, che li ha virtualmente suggeriti allo scienziato americano. Ci mise più di un anno Hofstadter per scrivere il dialogo in cui Achille e la Tartaruga, passeggiando, si scambiano opinioni sui gusti artistici (Escher è l’artista preferito di Achille), finché non incontrano il Granchio, il fattore G (Canone cancrizzante), il quale spiega come – per lui – avanzare oppure indietreggiare siano la stessa cosa. Il racconto prosegue allora con il medesimo dialogo scritto nella prima parte, ma invertito, ora incentrato sui gusti musicali (Bach è l’artista prediletto dalla Tartaruga), che riproduce le stesse frasi le quali, pur seguendo un ordine speculare, ossia rovesciato, riescono ad avere ugualmente senso. La struttura che ne deriva è quella di un ipotetico gene del «granChio» (GC), che è possibile leggere in questo modo:
TTTTTTTTTGCAAAAAAAAA
AAAAAAAAACGTTTTTTTTT
dove A è l’adenina, T la timina, ma «mirabile dictu», scrive Hofstadter, anche «Achille» e la «Tartaruga».
Punto centrale di questo Canone cancrizzante è un’opera di Escher del 1965 alla quale lo scienziato americano ha attribuito arbitrariamente tale titolo, ma che – in realtà – è l’acquarello 117 che rappresenta la tassellazione del piano utilizzando figure intervallate di granchi rosso-arancio e celeste-cenere che si alternano su file orientate secondo un verso opposto; il che, però, giustifica ampiamente la nuova intestazione proposta da Hofstadter.
Questo stesso modo di generare l’ordine, nel caso del DNA, biologico e in quello di Escher, spaziale – spiega lo scienziato americano – si ritrova in Johann Sebastian Bach e nelle sue composizioni musicali che si organizzano, sul pentagramma, secondo un ordine speculare (Hofstadter). Tutto questo accentua l’idea di mistero che irretiva Escher e anche noi, che siamo affascinati da lui.”
Una mostra e un catalogo su Escher possono essere ancora l’occasione per spiegare – soprattutto ai giovani – il retroterra del mondo visivo in cui siamo immersi?
“Mi auguro che la mostra, così come è stata impostata, con una serie di postazioni interattive, capaci di coinvolgere il pubblico di tutte le età (sono previste anche a dimensione di bambino), sia la maniera più diretta per entrare nel mondo di Escher dalla porta principale, quella del fare per capire e scorgere così quella profondità di pensiero che, spesso, l’artista presenta sul filo dell’ironia.”
Laureata e specializzata in storia dell’arte all’Università “La Sapienza” di Roma, ha svolto, tra 1989 e 2010, attività di studio, ricerca e didattica universitaria, come borsista, ricercatore e docente con il sostegno o presso i seguenti istituti, enti di ricerca e università: Accademia di San Luca, Comunità Francese del Belgio, CNR, ENEA, MIUR-Ministero della Ricerca, E.U-Unione Europea, Università Libera di Bruxelles, Università di Napoli-S.O Benincasa, Università degli Studi di Chieti-Università Telematica Leonardo da Vinci. Dal 2010 è CTU-Consulente Tecnico ed Esperto del Tribunale Civile e Penale di Roma. È autrice di articoli divulgativi e/o di approfondimento per vari giornali/ rubriche di settore e docente della 24Ore Business School.











lascia una risposta